Share

Enrichment Cascades 

by Ivanka Barzashka and Ivan Oelrich

No single existing centrifuge can enrich uranium from its natural concentration of about 0.7 percent uranium-235 to the 3 to 5 percent required to fuel a nuclear reactor.  In addition, the throughput of a centrifuge is very small compared to the consumption of a reactor. To multiply the effects of the enrichment of one machine and to achieve adequate throughput, large numbers of centrifuges are interconnected to form cascades.  The pattern of that connection is determined by the properties of the individual machines and the required quantity and concentration of the final product. An enrichment plant usually holds thousands of centrifuges.

Cascade Components

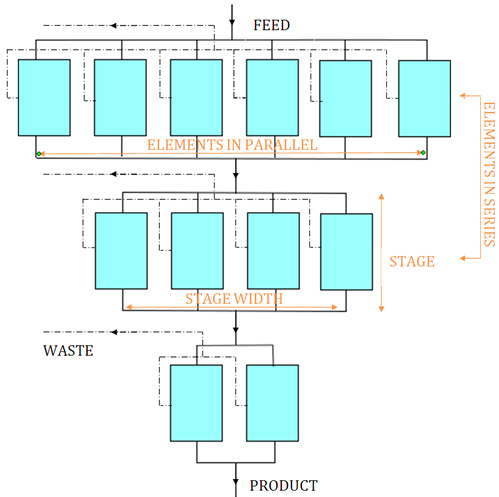
A cascade consists of separation units, in this case centrifuges, arranged in parallel that make up a single stage. The width of the cascade is the number of elements in a given stage. These elements receive identical feed and generate the same product and waste. The total flow rate through a stage determines the width of a stage because each individual machine is optimized for a given throughput. Therefore, to increase the throughput of a cascade, the number of machines per stage must be increased.

Simple Cascade

Stages are connected in series.  The desired concentration of the product determines the number of stages in the cascade.  The enriched output from each stage is passed on as input to the next stage . 

Enrichment in cascades is considered a continuous process, which means that the flow rates of the input and output of the stages are kept constant for the most part.

The external variables of a cascade are those that can be obtained without considering the internal mechanism and considering the cascade as a black box.  The same basic separation theory of an individual centrifuges applies to the overall cascade. The external variables of the cascade are the feed flowing at a rate of F and containing x_f  of the desired isotope, the product (or heads) flowing at a rate of P and containing x_p of the desired isotope and the waste (or tails) flowing at a rate of W and having a composition of x_w. The internal variables of the cascade include the interstage flow rates and compositions.

Cascade Types

In a simple cascade the waste stream of each stage is discarded, as shown in the picture above. However, the waste can be recycled and passed back down as input to a preceding stage in a recycle cascade [2] (or countercurrent cascade [3],[6]).  Almost all cascades recycle because it greatly increases the recovery of the uranium-235 extracted from a given quantity of natural uranium. A recycling cascade has two sections: the enriching section, consisting of the stages above the point at which the feed enters the cascade and the stripping section below the feed point. The stripping section increases the recovery of the material, whereas the enriching section produces material of increased concentration. A simple cascade has only an enriching section.

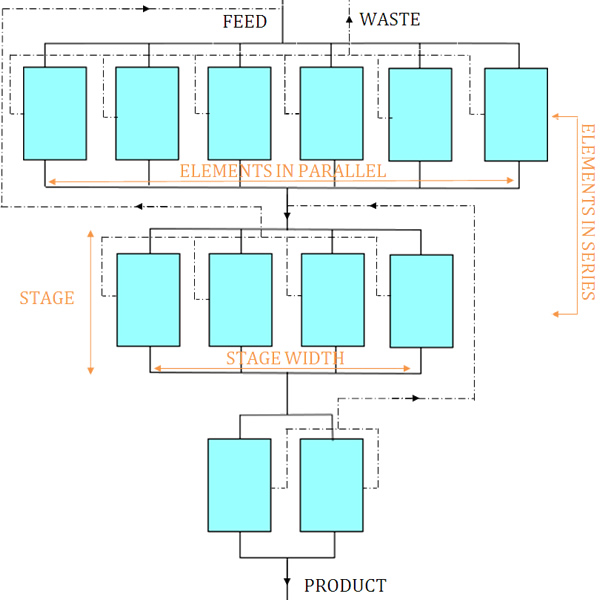
Symmetric Cascade

In a symmetric cascade, the waste stream is recycled back to the immediately preceding stage, as shown in the picture adjacent. In an asymmetric cascade, the waste is recycled more than one stage back. A common asymmetric cascade feeds the product stream into the next stage and sends the tails stream back two stages back. This is called a two-up, one-down cascade [5].  Asymmetric cascades were used in aerodynamic nozzle separation processes. While asymmetric cascades are rarely used for gas centrifuges [6], some authors argue that an asymmetric cascade can increase centrifuge cascade performance by about ten percent relative to a symmetric arrangement [5].

The material flow within a cascade determines the number of centrifuges per stage.  The material flow through a given stage is equal to the sum of the product flow of the previous stage and the waste flow of the next stage, which is in turn a function of the waste flow of the stage above that and so forth. The total material flow through a stage corresponds to the combined individual throughputs of the centrifuges that make up that stage.

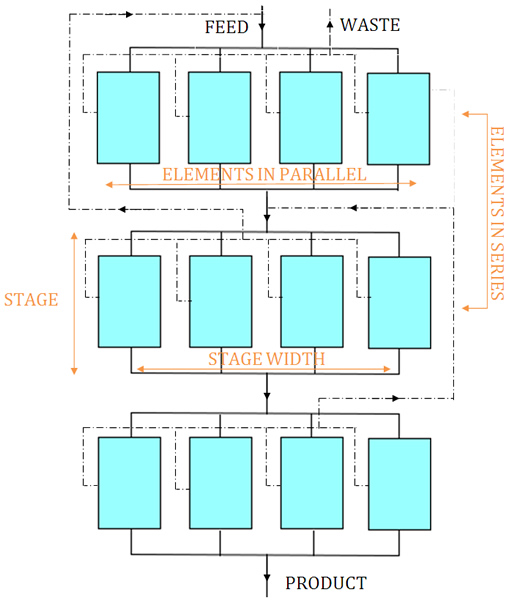
The number of separating units in most uranium enrichment cascades decreases with each stage towards the product and waste ends and this is known as a tapered cascade.  A square cascade has the same flow rates in all stages and therefore the same number of machines in each stage.

An ideal cascade, a type of tapered cascade, is the most efficient arrangement of centrifuges. It minimizes the total interstage flow rate and as a result uses the least number of machines to achieve the required separation by maximizing the separative work per separating element.  An ideal cascade has two important characteristics: it has the same separation factor for each stage and gases of different levels of enrichment are never mixed.  The first condition makes the use of identical machines possible thoughout the cascade.  The no mixing condition lowers energy consumption because no separative power is wasted by mixing flows of different concentrations.  To achieve this, the cuts of the stages are adjusted so the waste flow passed down to a stage has exactly the same isotopic concentration as the product flow being passed up from the preceding stage.  The ideal cascade has the shortest equilibrium time and the smallest inventory.

An ideal cascade is never achieved in practice.  Not every machine will perform exactly the same so the no-mixing rule is broken even within a stage.  Theoretically, the cut must be varied for each stage to keep different concentrations from mixing.  For an ideal cascade, the cut fluctuates very slightly around 0.5 but, in practice, these small fine adjustments in flow rates cannot be achieved.  Moreover, the theoretically optimal flow rate for every stage may correspond to a non-integer number of machines because centrifuges are optimized for a particular cut and throughput.  Obviously, it is not possible to operate a fraction of centrifuge, so machines will either have to work at non-optimum conditions to balance flow rates or there will be mixing of different isotope concentrations and, therefore, wasted separative work.  In practice, engineering tradeoffs among flow rate, cut, and separation factor are made to bring a real cascade as close as possible to ideal performance.

Square Cascade

A square cascade has the same flow rates in all stages and therefore the same number of machines per stage [4]. The arrangement is shown in the picture adjacent. Square cascades are rarely used because they are not very efficient; constant flow rate results in constant cut and mixing of concentrations and therefore loss of separative work. An ideal cascade can be approximated by linking several square cascades in what is called a squared-off cascade [4] that balances some loss of performance against simplicity in centrifuge design and performance calculation. Note that the terms square and squared-off cascade are sometimes used synonymously by some authors [2].

While building an individual centrifuge is itself a technical challenge, operating many machines together is also complex. The shape of a cascade varies with the overall enrichment goal, such as the amount and degree of enrichment, and is determined by both the separative capacity of a single machine and the properties of the feed and waste. Both internal and external variables can be optimized for best cascade performance. Good efficiency requires careful attention to flow rates and constant monitoring of individual centrifuge performance and output.

Maximum efficiency may not be the goal of an enrichment program, but instead the focus could be on speed or stealth. However, even a potential nuclear weapons proliferator cannot be indifferent to overall cascade performance, which determines the required amounts of input material and the time required to produce weapons-grade enriched uranium.

References: